I had the opportunity to participate in the Future Data Driven 2024 event (https://datadrivencommunity.com/FutureDataDriven2024.html) with my colleague Stéphane Haby.

Many speakers were present, and I was able to attend several sessions covering the following topics: Azure, AI, CosmosDB, Co-Pilot, Database Watcher. In several sessions, when AI was discussed, we talked about vector databases.
These were terms I had heard before but never really understood. So, I would like to present how vector databases are used.
Before talking about vector databases, it is necessary to cover certain concepts, which are as follows:
- Vectors
- Vector embeddings
- Cosine similarity
Vectors
General Information
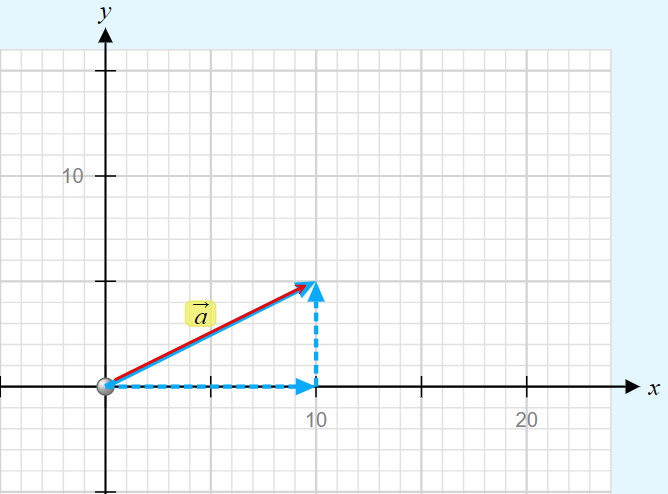
Vectors are mathematical objects that consist of both a magnitude (or length) and a direction. We can graphically represent a vector (in a 2-dimensional plane) as follows:
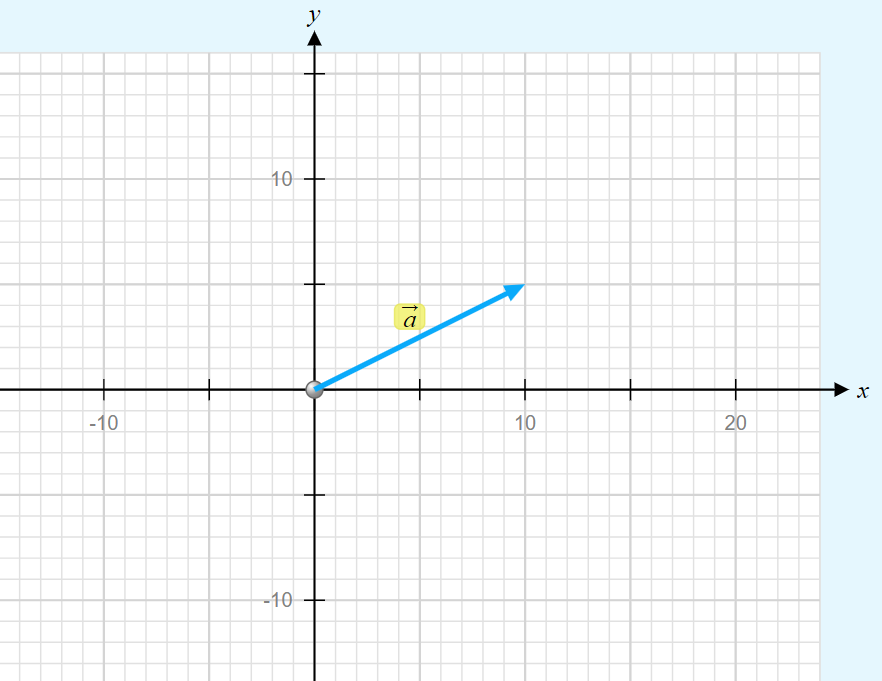
A 2-dimensional vector can be written as follows:
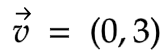
In our case, we can write it as:
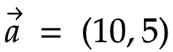
We also find another notation to describe vectors, which is as follows:
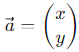
Vectors are multidimensional, and their notation can be as follows for a 4-dimensional vector:
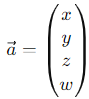
A first problem arises here. Indeed, when multiple vectors are described, this initial form of notation can be confusing. In this case, we can introduce a new notation:
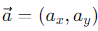
x and y are the components of vector a.
Length or Magnitude of a Vector:
We mentioned earlier that one of the properties of a vector is its length or norm. This is calculated as follows for a vector:
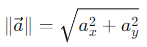
In the case of the vector described above, this results in:
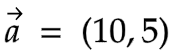
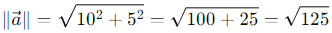
Thus, we can see that this formula corresponds to the calculation of the hypotenuse. The length of the vector is the value of the hypotenuse.
Vectors embeddings
Vector embeddings allow us to represent data (texts, images, etc.) in the form of vectors. One way to describe images using a relational database system would be to use several tables:
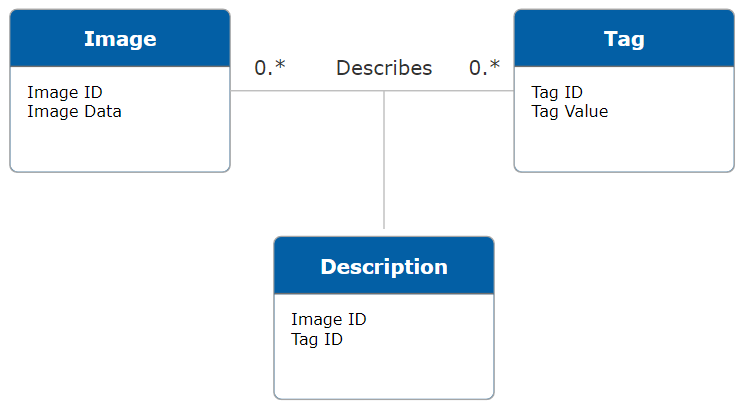
| Table name | Details |
|---|---|
| Image | Contains images |
| Tag | Contains words that describes images |
| Description | Associate an image with the words, the tags that describe it |
By using certain SQL operators, it should be possible to find images that are described as similar (because they share the same tags).
Vector embeddings represent data differently. Several techniques exist for this, including:
- Word2Vec: A method that uses neural networks to create vector representations of words.
- GloVe (Global Vectors for Word Representation): A technique that uses co-occurrence statistics to create embeddings.
- BERT (Bidirectional Encoder Representations from Transformers): An advanced model that generates contextual embeddings, taking into account surrounding words.
Thus, vector databases use vector embeddings. Once these embeddings are generated, they are stored in vector databases. Then, it is possible to use cosine similarity to evaluate how similar the vectors are. Finally, vector databases index the vectors, and there are several methods:
- Tree-based indexing
- Approximate Nearest Neighbors
- Quantization
Cosine similarity
Cosine similarity allows for a precise evaluation of the similarity between two vectors. Here is an example:
- Imagine that I have two recipe cards. I would like to determine if these two recipes are similar based on the ingredients mentioned in them.
- So, I have two recipes: R1 and R2
- R1: in this recipe, the word “egg” is mentioned 6 times and the word “flour” is mentioned 1 time.
- R2: in this recipe, the word “egg” is mentioned 1 time and the word “flour” is mentioned 8 times.
- So, I have two recipes: R1 and R2
Based on this information, it is possible to graphically represent how many times these words appear.
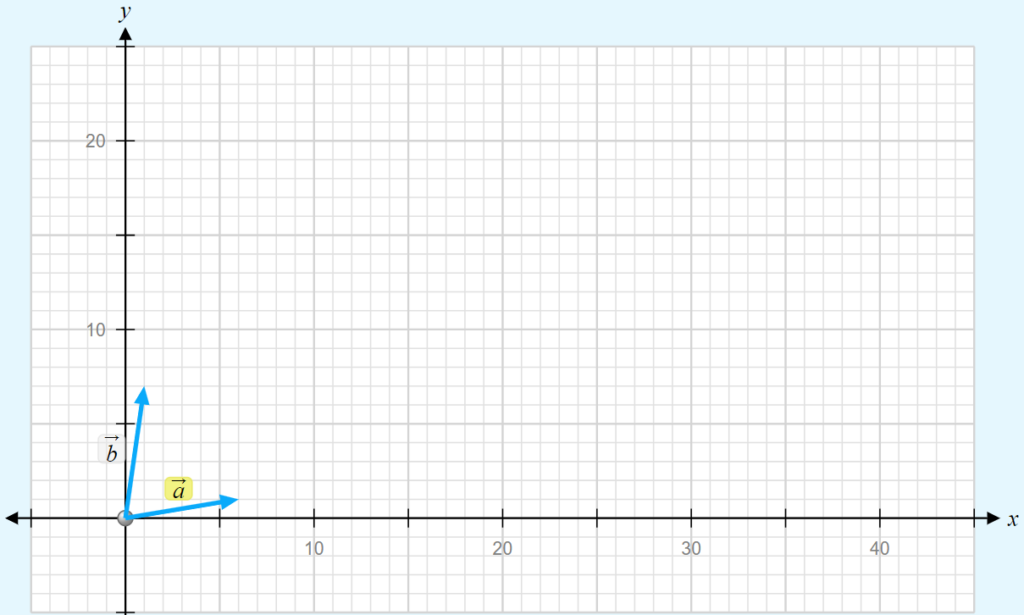
The first vector represents my first recipe. The second vector represents my second recipe.
Cosine similarity will determine if these two recipes are similar (this is a very simplified example). To do this, we need to calculate the cosine of 81 degrees (which is 0.15643447). Here, on the graph, the angle formed between the two vectors is 81 degrees.
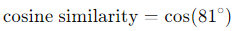
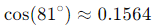
Here are more details on how to calculate cosine similarity:
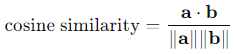
It is possible to represent recipes R1 and R2 by two vectors, which are as follows:
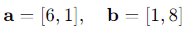
So we have:
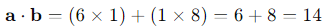
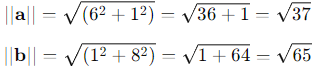
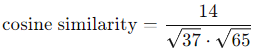
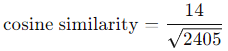
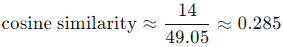
The values of cosine similarity can range between -1 and 1. Here, this value indicates that the two recipes are not very similar.
Pinecone, vector databases, python implementation
Pinecone is a vector database. It is designed to store, manage, and search vectors, enabling similarity search operations and analyses based on unstructured data.
Here is an example created from the documentation that illustrates how to use vector databases and calculate similarities between vectors:
Code :
from pinecone.grpc import PineconeGRPC as Pinecone
from pinecone import ServerlessSpec
pc = Pinecone(api_key='MyAPIKey')
index_name = "example-index"
pc.create_index(
name=index_name,
dimension=2,
metric="cosine", #we use the cosine similarity
spec=ServerlessSpec(
cloud='aws',
region='us-east-1'
)
)
while not pc.describe_index(index_name).status['ready']:
time.sleep(1)
index = pc.Index(index_name)
index.upsert(
vectors=[
{"id": "vec1", "values": [6,1]}, #we define our first vector
{"id": "vec2", "values": [1,8]}, #we define our second vector
],
namespace="example-namespace1"
)
query_results1 = index.query(
namespace="example-namespace1",
vector=[1,7],
top_k=3,
include_values=True
)
print(query_results1)Here is the result:
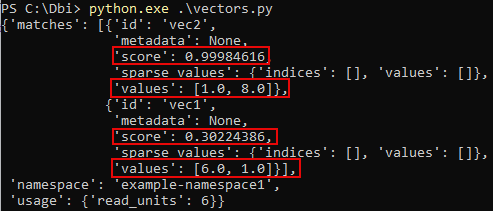
We had as input a vector with the value of [1, 7]. This vector was compared to the other two vectors, and the cosine similarity (the score) was determined.
If you encounter any errors while running this script, it is possible that your index already exists or has not yet been created.
Thank you, Amine Haloui.
![Thumbnail [60x60]](https://www.dbi-services.com/blog/wp-content/uploads/2024/03/AHI_web.jpg)
![Thumbnail [90x90]](https://www.dbi-services.com/blog/wp-content/uploads/2022/10/STS_web-min-scaled.jpg)
![Thumbnail [90x90]](https://www.dbi-services.com/blog/wp-content/uploads/2022/08/STH_web-min-scaled.jpg)